I came across this excerpt from a a christian home schooling book:
Wednesday, January 24, 2024
How do magnets work?
Monday, November 13, 2023
How not to detect MOND
You might have heard about recent efforts to inspect lots of "wide binaries", double stars that orbit each other at very large distances, which is one of the tasks the Gaia mission was built for, to determine if their dynamics follows Newtonian gravity or rather MOND, the modified Newtonian dynamics (Einstein theory plays no role at such weak fields).
You can learn about the latest update from this video by Dr. Betty (spoiler: Newton's just fine).
MOND is an alternative theory of gravity that was originally proposed as an alternative to dark matter to explain galactic rotation curves (which it does quite well, some argue better than dark matter). Since, it has been investigated in other weak gravity situations as well. In short, it introduces an additional scale \(a_0\) of dimension acceleration and posits that gravitational acceleration (either in Newton's law of gravity or in Newton's second law) are weakened by a factor
$$\mu(a)=\frac{a}{\sqrt{a^2+a_0^2}}$$
where a is the acceleration without the correction.
In the recent studies reported on in the video, people measure the stars' velocities and have to do statistics because they don't know about the orbital parameters and the orientation of the orbit relative to the line of sight.
That gave me an idea of what else one could try: When the law of gravity gets modified from its \(1/r^2\) form for large separations and correspondingly small gravitational accelerations, the orbits will no longer be Keppler ellipses. What happens for example if this modified dynamics would result for example in eccentricities growing or shrinking systematically? Then we might observe too many binaries with large/small eccentricities and that would be in indication of a modified gravitational law.
The only question is: What does the modification result in? A quick internet search did not reveal anything useful combining celestial mechanics and MOND, so I had to figure out myself. Inspection shows that you can put the modification into a modification of \(1/r^2\) into
$$\mu(1/r^2) \frac{\vec r}{r^3}$$
and thus into a corresponding new gravitational potential. Thus much of the usual analysis carries over: Energy and angular momentum would still be conserved and one can go into the center of mass system and work with the reduced mass of the system. And I will use units in which \(GM=1\) to simplify calculations.
The only thing that will no longer be conserved is the Runge-Lenz-vector
$$\vec A= \vec p\times\vec L - \vec e_r.$$
\(\vec A\) points in the direction of the major semi-axis and its length equals the eccentricity of the ellipse.
Just recall that in Newton gravity, this is an additional constant of motion (which made the system \(SO(4,2)\) rather than \(SO(3)\) symmetric and is responsible for states with different \(\ell\) being degenerate in energy for the hydrogen atom), as one can easily check
$$\dot{\vec A} = \{H, \vec A\}= \dot{\vec p}\times \vec L-\dot{\vec e_r}=\dots=0$$
using the equations of motion in the first term.
To test this idea I started Mathematica and used the numerical ODE solver to solve the modified equations of motion and plot the resulting orbit. I used initial data that implies a large eccentricity (so one can easily see the orientation of the ellipse) and an \(a_0\) that kicks in for about the further away half of the orbit.
 |
| Orbit of would be Runge Lenz vector \(\vec A\) |
What a disappointment! Even if it is no longer conserved it seems to move on a circle with some additional wiggles on it (Did anybody mention epicycles?). So it is only the orientation of the orbit that changes with time but there is no general trend toward smaller or larger eccentricities that one might look out for in real data.
On the other hand the eccentricity \(\|\vec A\|\) is not exactly conserved but wiggles a bit with the orbit but comes back to its original value after one full rotation. Can we understand that analytically?
To this end, we make use the fact that the equation of motion is only used in the first term when computing the time derivative of \(\vec A\):
$$\dot{\vec A}=\left(1-\mu(1/r^2)\right) \dot{\vec e_r}.$$
\(\mu\) differs from 1 far away from the center, where the acceleration is weakest. On the other hand, since \(\vec e_r\) is a unit vector, its time derivative has to be orthogonal to it. But in the far away part of the the ellipse, \(\vec e_r\) is almost parallel to the major semi axis and thus \(\vec A\) and thus \(\dot{\vec a}\) is almost orthogonal to \(\vec A\). Furthermore, due to the reflection symmetry of the ellipse, the parts of \(\dot{\vec e_r}\) that are not orthogonal to \(\vec A\) will cancel each other on both sides and thus the wiggling around the average \(\|\vec a\|\) is periodic with the period of the orbit. q.e.d.
There is only a tiny net effect since the ellipse is not exactly symmetric but precesses a little bit. This can be seen when plotting \(\|\vec A\|\) as a function of time:
 | |
|
 | |
|
Friday, April 28, 2023
Can you create a black hole in AdS?
Here is a little puzzle I just came up with when in today's hep-th serving I found
arXiv:2304.14351 [pdf, other] When two particles collide in an asymptotically AdS spacetime with high enough energy and small enough impact parameter, they can form a black hole.
But to explain it, I should probably say one or two things about thermal states in the algebraic QFT language: There (as we teach for example in our "Mathematical Statistical Physics" class) you take take to distinguish (quasi-local) observables which form a C*-algebra and representations of these on a Hilbert space. In particular, like for example for Lie algebras, there can be inequivalent representations that is different Hilbert spaces where the observables act as operators but there are no (quasi-local) operators that you can use to act on a vector state in one Hilbert space that brings you to the other Hilbert space. The different Hilbert space representations are different super-selection sectors of the theory.
A typical example are states of different density in infinite volume: The difference in particle number is infinite but any finite product of creation and annihilation operators cannot change the particle number by an infinite amount. Or said differently: In Fock space, there are only states with arbitrary but finite particle number, trying to change that you run into IR divergent operators.
Similarly, assuming that the (weak closure) of the representation on one Hilbert space if a type III factor as it should be for a good QFT, states of different temperatures (KMS states in that language) are disjoint, meaning they live in different Hilbert spaces and you cannot go from one to the other by acting with a quasi-local operator. This is proven as Theorem 5.3.35 in volume 2 of the Bratelli/Robinson textbook.
Now to the AdS black holes: Start with empty AdS space also encoded by the vacuum in the holographic boundary theory. Now, at t=0 you act with two boundary operators (obviously quasi-local) to create two strong gravitational wave packets heading towards each other with very small impact parameter. Assuming the hoop conjecture, they will create a black hole when they collide (probably plus some outgoing gravitational radiation).
Then we wait long enough for things to settle (but not so long as the black hole starts to evaporate in a significant amount). We should be left with some AdS-Kerr black hole. From the boundary perspective, this should now be a thermal state (of the black hole temperature) according to the usual dictionary.
So, from the point of the boundary, we started from the vacuum, acted with local operators and ended up in a thermal state. But this is exactly what the abstract reasoning above says is impossible.
How can this be? Comments are open!
Saturday, November 26, 2022
Get Rich Fast
I wrote a text as a comment on the episode of the Logbuch Netzpolitik podcast on the FTX debacle but could not post it to the comment section (because that appears to be disabled). So in order not to waste I post it here (in German):
1. Hebel (leverage): Wenn ich etwa glaube, dass in Zukunft die Appleaktie weiter steigen wird, kann ich mir eine Appleaktie kaufen, um davon zu profitieren. Die kostet momentan etwa 142 Euro, kaufe ich eine und steigt der Preis auf 150 Euro habe ich natürlich 8 Euro Gewinn gemacht. Besser natürlich noch, wenn ich 100 kaufe, dann mache ich 800 Euro Gewinn. Hinderlich ist dabei nur, wenn ich nicht 14200 Euro dafür zur Verfügung habe. Aber kein Problem, dann nehme ich eben einen Kredit über den Preis von 99 Aktien (also 14038 Euro) auf. Der Einfachheit halber ignorieren wir mal, dass ich dafür Zinsen zahlen muss, die machen das ganze Spiel für mich nur unattraktiver. Ich kaufe also 100 Aktien, davon 99 auf Pump. Ist der Kurs bei 150, verkaufe ich sie wieder, zahle den Kredit ab und gehe mit 800 Euro mehr nach Hause. Ich habe also den Kursgewinn verhundertfacht.
Doof nur, dass ich gleichzeitig auch das Verlustrisiko verhundertfache: Fällt der Aktienkurs entgegen meiner optimistischen Erwartungen, kann es schnell sein, dass ich beim Verkauf der Aktien nicht mehr genug Geld zusammenbekomme, um den Kredit abzuzahlen. Das tritt dann ein, wenn die 100 Aktien weniger wert sind, als der Kredit, wenn also der Aktienwert unter 140,38 Euro fällt. Wenn ich in dem Moment meine Aktien verkaufe, kann ich grade noch meine Schulden bezahlen, habe aber mein Eigenkaptial, das war die eine Aktie, die ich von meinem eigenen Geld gekauft habe, komplett verloren. Ist der Kurs aber noch tiefer gefallen, kann ich beim Spekulieren auf Pump aber mehr als all mein Geld verlieren, ich habe nichts mehr, aber immer noch nicht meine Schulden abbezahlt. Davor hat aber natürlich auch die Bank, die mir den Kredit gegeben hat, Angst, daher zwingt sie mich spätestens, wenn der Kurs auf 140,38 gefallen ist, die Aktien zu verkaufen, damit sie auf jeden Fall ihren Kredit zurück bekommt. Daniel nennt das "glattstellen".
2. Das finde ich natürlich blöd, weil der Kurs viel schneller mal um diese 1,42 Euro fällt, als dass er um 8 Euro steigt. Um das zu verhindern, kann ich bei der Bank noch andere Dinge von Wert hinterlegen, zB mein iPhone, das noch 100 Euro wert ist. Dann zwingt mich die Bank erst meine Aktien zu verkaufen, wenn der Wert der Aktien plus den 100 Euro für das iPhone unter den Wert des Kredits fällt. Sie könnte ja immer noch das iPhone verkaufen, um ihr Geld zurück zu bekommen. Wenn ich aber kein iPhone zum Hintelegen habe, muss ich etwas anderes werthaltiges bei der Bank hinterlegen (collateral).
3. Hier kommen die Tokens ins Spiel. Ich kann mir 1000 Kryptotokens ausdenken (ob mit dem Besitz von computergenerieren Cartoons von Tim und Linus verknüpft ist dabei egal). Da ich mir die nur ausgedacht habe, bin ich noch nicht weiter, so haben sie ja keinen Wert. Ich kann versuchen, sie zu verkaufen, aber dabei werde ich nur ausgelacht. Hier kommt meine zweite Firma, der Investment Fond ins Spiel: Mit dem kaufe ich mir selber 100 der Tokens zum Preis von 30 Euro das Stück ab. Wenn jetzt nicht klar ist, dass ich mir selber die Dinger abgekauft habe (ggf. über einen Strohmann:in) sieht es so aus, als würden die Tokens ernsthaft für einen Wert von 30 Euro gehandelt. Ausserdem verkaufe ich noch den Kunden meines Fonts 100 weitere auch für 30 Euro mit dem Versprechen, dass die Besitzer der Coins Rabatt auf die Gebühren meines Fonds bekommen. Spätestens jetzt ist der Wert von 30 Euro pro Token etabliert. Ich habe von den ursprünglichen 1000 immer noch 800. Jetzt kann ich behaupten, ich habe Besitz im Wert von 24000, denn das sind 800 mal 30 Euro. Diesen Besitz habe ich quasi aus dem Nichts geschaffen, da die Annahme, dass ich auch noch echte Käufer für die anderen 800 bei diesem Preis finden kann, Quatsch ist.
Wenn ich das ganze aber nur gut genug verschleiere, glaubt mir vielleicht jemand, dass ich wirklich auf Werten von 24000 Euro sitze. Insbesonder die Bank aus Schritt 1 und 2 glaubt mir das vielleicht und ich kann diese Tokens als Sicherheit für den Kredit hinterlegen und damit noch höhere Kredite aufnehmen, um damit Apple-Aktien zu kaufen.
Das ganze fliegt erst auf, wenn der Kurs der Aktien so weit fällt, dass die Bank darauf besteht, dass der Kredit zurück gezahlt werden muss. Dann muss ich eben nicht nur die Aktien und das iPhone verkaufen, sondern auch noch die weiteren Tokens. Und dann stehe ich eben ohne Hose da, weil dann klar wird, dass natürlich niemand die Tokens, die ich mir einfach ausgedacht habe, haben will, schon gar nicht für 30 Euro. Dann fehlt in den Worten von Daniel die "Liquidität".
Das ist nach meinem Verständnis, was passiert ist, natürlich nicht mit Apple-Aktien und iPhones, aber im Prinzip. Und der Sinn des mit sich selbst Geschäfte-im-Kreis machen, ist eben, damit künstlich die scheinbaren Preise von etwas, wovon ich noch mehr habe, in die Höhe zu treiben. Der Fehler des ganzen ist, dass schwierig ist, die Werte von etwas zu beurteilen, was gar nicht wirkich gehandelt wird, bzw wo der Wert nur auf anderen angenommenen Werten beruht, wobei sich die Annahmen über die Werte sehr schnell ändern können, wenn jemand "will sehen!" sagt und keine realen Werte (wie traditionell in Form von Fabriken, Know-How etc) dahinter liegen.
Tuesday, October 04, 2022
No action at a distance, spooky or not
On the occasion of the announcement of the Nobel prize for Aspect, Clauser and Zeilinger for the experimental verification that quantum theory violates Bell's inequality, there seems to be a strong urge in popular explanations to state that this proves that quantum theory is non-local, that entanglement is somehow a strong bond between quantum systems and people quote Einstein on the "spooky action at a distance".
But it should be clear (and I have talked about this here before) that this is not a necessary consequence of the Bell inequality violation. There is a way to keep locality in quantum theory (at the price of "realism" in a technical sense as we will see below). And that is not just a convenience: In fact, quantum field theory (and the whole idea of a field mediating interactions between distant entities like the earth and the sun) is built on the idea of locality. This is most strongly emphasised in the Haag-Kastler approach (algebraic quantum field theory), where pretty much everything is encoded in the algebras of observables that can be measured in local regions and how these algebras fit into each other. So throwing out locality with the bath water removes the basis of QFT. And I am convinced this is the origin why there is no good version of QFT in the Bohmian approach (which famously sacrifices locality to preserve realism, something some of the proponents not even acknowledge as an assumption as it is there in the classical theory and it needs some abstraction to realise it is actually an assumption and not god given).
But let's get technical. To be specific, I will use the CHSH version of the Bell inequality (but you could as well use the original one or the GHZ version as Coleman does). This is about particles that have two different properties, here termed A and B. These can be measured and the outcome of this measurement can be either +1 or -1. An example could be spin 1/2 particles and A and B representing twice the components of the spin in either the x or the y direction respectively.
Now, we have two such particles with these properties A and B for particle 1 and A' and B' for particle 2. CHSH instruct you to look at the expectation value of the combined observable
\[A (A'+B') + B (A'-B').\]
Let's first do the classical analysis: We don't know about the two properties of particle 2, in the primed variables. But we know, they are either equal or different. In case they are equal, the absolute value of A'+B' is 2 while A'-B'=0. If they are different, we have A'+B'=0 while the absolute value of A'-B' is two. In either case, one one of the two terms contribute and in absolute value it is 2 times the unprimed observable of particle one, A for equal values in particle 2 an B for different values for particle 2. No matter which possibility is realised, the absolute value of this observable is always 2.
If you allow for probabilistic outcomes of the measurements, you can convince yourself that you can also realise smaller absolute values than 2 but never larger ones. So much for the classical analysis.
In quantum theory, you can, however, write down an entangled state of the two particle system (in the spin 1/2 case specifically) where this expectation value is 2 times the square root of 2, so larger than all the possible classical values. But didn't we just prove it cannot be larger than 2?
If you are ready to give up locality you can now say that there is a non-local interaction that tells particle 2 if we measure A or B on particle one and by this adjust its value that is measured at the site of particle two. This is, I presume, what the Bohmians would argue (even though I have never seen a version of this experiment spelled out in detail in the Bohmian setting with a full analysis of the particles following the guiding equation).
But as I said above, I would rather give up realism: In the formula above and the classical argument, we say things like "A' and B' are either the same or opposite". Note, however, that in the case of spins, you cannot both measure the spin in x and in y direction on the same particle because they do not commute and there is the uncertainty relation. You can measure either of them but once you decided you cannot measure the other (in the same round of the experiment). To give up realism simply means that you don't try to assign a value to an observable that you cannot measure because it is not compatible with what you actually measure. If you measure the spin in x direction it is no longer the case that the spin in the y direction is either +1/2 or -1/2 and you just don't know because you did not measure it, in the non-realistic theory you must not assign any value to it if you measured the x spin. (Of course you can still measure A+B, but that is a spin in a diagonal direction and then you don't measure either the x nor the y spin).
You just have to refuse to make statements like "the spin in x and y directions are either the same or opposite" as they involve things that cannot all be measured, so this statement would be non-observable anyways. And without these types of statement, the "proof" of the inequality goes down the drain and this is how the quantum theory can avoid it. Just don't talk about things you cannot measure in principle (metaphysical statements if you like) and you can keep our beloved locality.
Thursday, July 21, 2022
Giving the Playground Express a Spin
The latest addition to our single chip computer zoo is Adafruit's Circuit Playground Express. It is sold for about 30$ and comes with a lot of GIO pins, 10 RGB LEDs, a small speaker, lots of sensors (including acceleration, temperature, IR,...) and 1.5MB of flash rom. The excuse for buying it is that I might interest the kids in it (being better equipped on board than an Arduino while being less complex than a RaspberryPi.
As the ten LEDs are arranged around the circular shape, I thought a natural idea for a first project using the accelerometer would be to simulate a ball going around the circumference.
// A first project simulating a ball rolling around the Playground Express#include <Adafruit_CircuitPlayground.h>uint8_t pixeln = 0;float phi = 0.0;float phid = 0.10;void setup() {CircuitPlayground.begin();CircuitPlayground.speaker.enable(1);}int phi2pix(float alpha) {alpha *= 180.0 / 3.141459;alpha += 60.0;if (alpha < 0.0)alpha += 360.0;if (alpha > 360.0)alpha -= 360.0;return (int) (alpha/36.0);}void loop() {static uint8_t lastpix = 0;float ax = CircuitPlayground.motionX();float ay = CircuitPlayground.motionY();phid += 0.001 * (cos(phi) * ay - sin(phi) * ax);phi += phid;phid *= 0.997;Serial.print(phi);while (phi < 0.0)phi += 2.0 * 3.14159265;while (phi > 2.0 * 3.14159265)phi -= 2.0 * 3.14159265;pixeln = phi2pix(phi);if (pixeln != lastpix) {if (CircuitPlayground.slideSwitch())CircuitPlayground.playTone(2ssseff000, 5);lastpix = pixeln;}CircuitPlayground.clearPixels();CircuitPlayground.setPixelColor(pixeln, CircuitPlayground.colorWheel(25 * pixeln));delay(0);}
Saturday, July 09, 2022
Voting systems, once more
Over the last few days, I have been involved in some heated Twitter discussions around a possible reform of the voting system for the German parliament. Those have sharpened my understanding of one or two things and that's why I think it's worthwhile writing a blog post about it.
The root of the problem is that the system currently in use tries to optimise two goals which are not necessarily compatible: Proportional representation (number of seats for a party should be proportional to votes received) and local representation (each constituency being represented by at least one MP). If you only wanted to optimise the first you would not have constituencies but collect all votes in one big bucket and assign seats accordingly to the competing parties, if you only wanted to optimise the second goal you would use a first past the pole (FPTP) voting system like in the UK or the US.
In a nutshell (glancing over some additional complications), the current system is as follows: We start by assuming there are twice as many seats in parliament as there are constituencies. Each voter has two different votes. The first is a FPTP vote that determines a local candidate that will definitely get a seat in parliament. The second vote is the proportional vote that determines the percentage of seats for the parties. The parties will then send further MPs to reach their allocated lot but the winners of the constituencies are counted as well and the parties only "fill up" the remaining seats from their party list. So far so good, you have achieved both goals: There is one winner MP from each constituency and the parties have seats proportional to the number of (second) votes. Great.
Well, except if a party wins more constituencies than they are assigned seats according to proportional votes. This was not so much of a problem some decades ago when there were two major parties (conservative and social democrat) and one or two smaller ones. The two parties would somehow share the constituency wins but since those make up only half of the total number of seats those would not be many more than their share to total seats (which would typically be well above 30% or even 40%).
The voting system's solution to this problem is to increase the total number of seats to the minimal total number such that each party's number of won constituencies is at least as high as their shore of total seats according to proportional vote.
But these days, the two former big parties have lost a lot of their support (winning only 20-25% in the last election) and four additional parties being also represented and not getting much less votes than the two former big ones. In the constituencies it is not rare that you win your FPTP seat with less than 30% of the votes in the constituency and it the last election it can be as low as only 18% sufficient to being the winner of a seat. This lead to the parliament having 736 seats as compared to the nominal size of 598 and there were polls not long before that election which suggested 800+ seats or possibly even over 1000.
A particular case is the CSU, the conservative party here in Bavaria (which is nominally a different party from the CDU, which is the conservative party in the rest of Germany. In Bavaria, the CDU is not competing while in the rest of the country, the CSU is not on the ballot): Still being relative winners here, they won all but one constituencies but got only about 30% of the votes in Bavaria which translates to slightly above 5% of all votes in Germany.
According to a general sentiment, 700+ seats is far too big (for a functioning parliament and also cost wise), so the system should be reformed. But people differ on how to reform it. A simple solution mathematically would be to increase the size of the constituencies to decrease their total number. So the total number of constituency winners to be matched by proportional votes would be less. But that solution is not very popular with the main argument being that those constituents would be too big for a reasonable contact of the local MPs to their constituents. Another likely reason nobody really likes to talk about is that by redrawing district lines by a lot would probably cause a lot of infighting in all the parties because the candidatures would have to be completely redistributed with many established candidates losing their job. So that is off the table, after all, it's the parties in parliament which decide about the voting system by simple majority (with boundary conditions set by relatively vague rules set by the constitution).
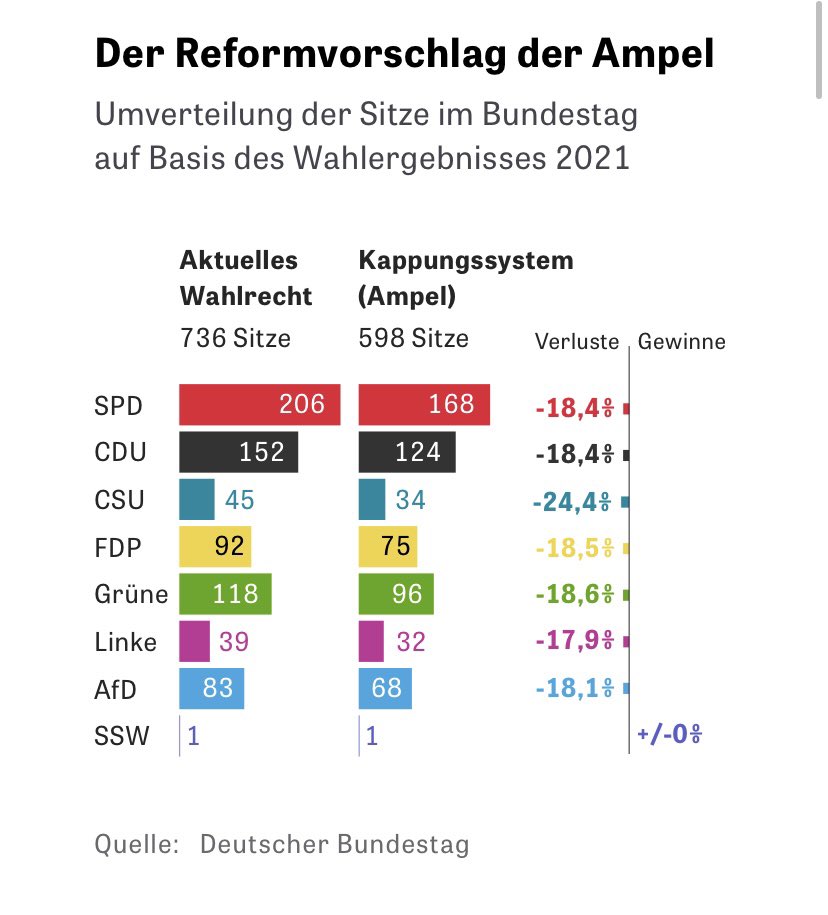
There is now a proposal by the governing social democrat-green-liberal coalition. The main idea is to weaken the FPTP system in the constituencies maintaining the proportional vote: Winning a constituency no longer guarantees you a seat in parliament. If you party wins more constituencies than their share of total seats according to the proportional votes, those constituency seats where the party's relative majority was the smallest would be allocated to the runner up (as that candidates party still has to be allocated seats according to proportional vote). This breaks FPTP, but keeps the proportional representation as well as the principle of each constituency sending at least one MP while fixing the total number of seats in parliament to the magic 598.
The conservatives in opposition do not like this idea (been traditionally the relatively strongest parties and thus tending to win more constituencies). You can calculate how many seats each party would get assuming the last election's votes: All parties would have to give up about 18% of their seats except for the CSU, the Bavarian conservatives, who would lose about 25% since some fine print I did not explain so far favours parties winning relatively many constituencies directly.
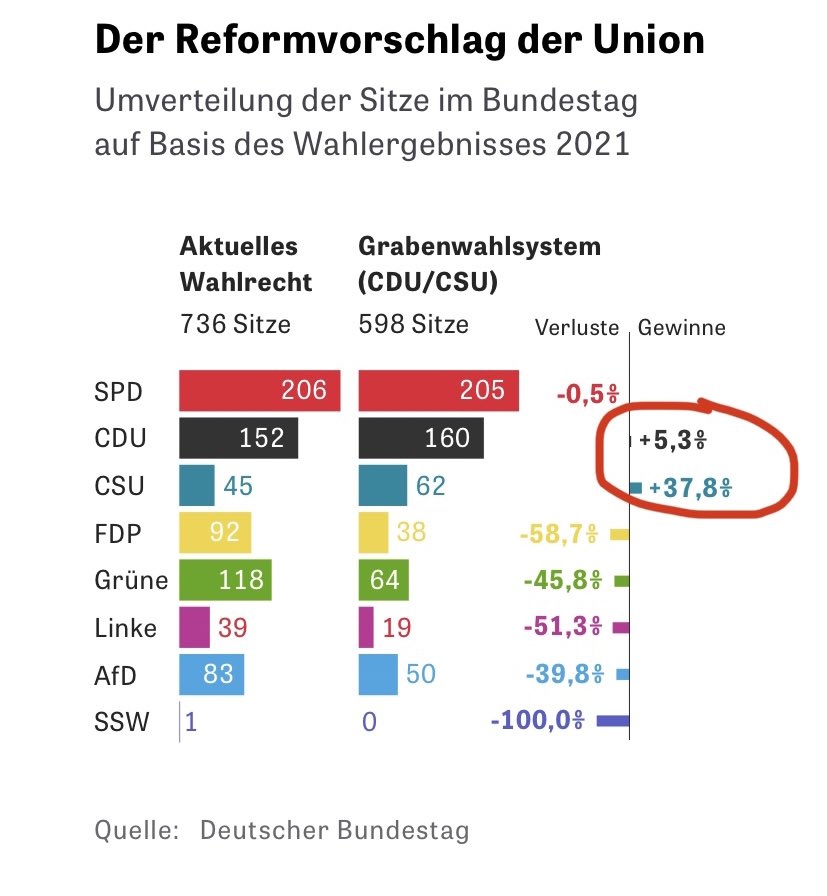
The conservatives also have a proposal. They are willing to give up proportionality in favour of maintaining FPTP and fixing the number of seats to 598: They propose to assign 299 of the seats according to FPTP to constituency winners and only distributing the remaining 299 seats proportionally. So they don't want to include the constituency winners in the proportional calculation.
This is the starting point of the Twitter discussions. Both sides accusing the other side have an undemocratic proposal. One side says a parliament where the majorities do not necessarily (and with current data) unlikely represent majorities in the population is not democratic while the other side arguing that denying a seat to a candidate that won his/her constituency (even by a small relative majority) being not democratic.
Of course it is a total coincidence that each side is arguing for the system that would be better for them (the governing coalition hurting everybody almost equally only the CSU a bit more while the conservative proposal actually benefitting the conservatives quite a bit while in particular hurting the smaller parties that do not win many constituencies or none at all).
(Ampel being the governing coalition, Union being the conservative parties).
Of course, both proposals are in a mathematical sense "democratic" each in their own logic emphasising different legitimate aspects (accurate proportional representation vs accurate representation of local winners).
Beyond the understandable preference for a system that favours one's own political side I think a more honest discussion would be about which of these legitimate aspects is actually more relevant for the political discourse. If a lot of debates would be along geographic lines, north against south, east against west or even rural vs urban then yes, it is very important that the local entities are as accurately represented as possible to get the outcomes of these debates right. That would emphasise FPTP as making sure local communities are most honestly represented.
If however typical debates are along other fault lines, for example progressive vs conservative or pro business vs pro social wealth redistribution then we should make sure the views of the population are optimally represented. And that would be in favour of a strict proportional representation.
Guess what I think is actually the case.
All that in addition to a political tradition in which "calling your local MP or representative" is a much less common thing that in anglo-saxon countries and studies showing that even shortly after a general election less than a quarter of the voters being able to name at least two of the names of their constituency's candidates casting serious doubts about an informed decision at the local level rather than along party lines (where parties being only needed to make sure there is only one candidate per party in the FPTP system while being the central entity for proportional votes).
PS: The governing coalition's proposal has some ambiguities as well (as I demonstrate here --- in German).